Wachu - DevLog

Witam, dzisiaj przedstawie rozwiazanie problemu testowania kolizji obb za pomoca konstrukcji 3-ciej metryki. Nasz rysunek pomocniczy wyglada w tak:


Metryki d1, d2 przedstawiaja przykladowe kule w metrykach opisujacych obb. Metryka d3 jest tworzona na podstawie dwoch poprzednich. Na rysunku na szaro sa zaznaczone odpowiednio metryki d1' i d2' czyli lekko zmodyfikowane metryki d1 i d2. Metryka d3 powstaje przez maximum z metryk d1' i d2', a zostaje ona wyznaczona przez krzywa ktora zakresla srodek obb w momencie stykania sie z drugim obb ( konsekwencja pomyslu ze jeden obb powiekszamy, a drugi zmniejszamy do punktu - czyli srodka ). Problem jaki sie pojawia mozna latwo odgadnac z rysunku: o jaki promien powinnismy rozszerzyc kazda z metryk, aby otrzymac metryke d3? Aby odpowiedziec na to pytanie musimy zdefiniowac metryke dla prostokata:

• max{ |(c1.x - x) cos(-α) - (c1.x - x) sin(-α)| , |(c1.y - y) sin(-α) + (c1.y - y)cos(-α)| * f}

Jak widac jest to standardowa metryka, tyle ze dodalismy wspolczynnik f wyrazony jako stosunek szerokosci prostokata do jego wysokosci ( czyli promien jest jego szerokoscia, a r / f wysokoscia ). Teraz bierzemy dwa wierzcholki obb podstawiamy ich wspolrzedne do metryki drugiego obb ( wzgledem srodka pierwszego obb) obliczamy jego odleglosc po x i po y, bierzemy max z x'ow i max z y'kow. Obliczamy wspolczynnik proporcjonalnosci dla nowych metryk d1' i d2'. Promienie obb powiekszamy o max z x'ow i testujemy czy srodek jednego obb nalezy do kuli w metryce d3.

Testowy program i kod: http://www.ex_xerox.republika.pl/test.rar

Chcialbym przedstawic rozwiniecie sposobu na wykrycie kolizji metoda rozwiazania ukladu rownan:
max{ |(c1.x - x) cos(-α) - (c1.x - x) sin(-α)| , |(c1.y - y) sin(-α) + (c1.y - y)cos(-α)| } = r1
max{ |(c2.x - x) cos(-β) - (c2.x - x) sin(-β)| , |(c2.y - y) sin(-β) + (c2.y - y)cos(-β)| } = r2

Jak widac rozwiazanie tego ukladu nie jest proste(wiele przypadkow). Najlepszym sposobem byloby tylko okreslenie czy uklad ma rozwiazanie.

OBB mozna przedstawic rowniez za pomoca innej metryki:

• d(a, b) = |(a.x - b.x) cos(-φ-π/4) - (a.x - b.x) sin(-φ-π/4)| + |(a.y - b.y) sin(-φ-π/4) + (a.y - b.y)cos(-φ-π/4)|

Nie jestem przekonany czy to prostszy sposob :)

Przedstawione tutaj metody maja jedna wspolna wade: nie poprawiaja zlozonosci obliczeniowej w stosunku do najprostrzego podejscia wykrywania kolizji obb(policzenie rownan prostych przechodzacych przez wierzcholki obb i rozwiazanie ukladow rownan). Jedyna zaleta przedstawionej metody jest taka, ze w ogole nie trzeba znac pozycji wierzchokow.

Jesli ta metoda bedzie w przyszlosci przezemnie rozwijana to pewnie tylko w kierunku szacowania ilosci rozwiazan.

Witam po dluzszej przerwie! Ostatnio mowilem o zastosowaniu przestrzeni metrycznych w wykrywaniu kolizji obb - obb.

Wynikiem tych rozwazan jest maly programik prezentujacy dzialanie tych kolizji w prkatyce... wynik jest daleki od idealu, bo nie dokladny. Na lepsza wersje tego programu + zrodla bedzie trzeba jeszcze poczekac. Test pokazuje za to ze samo wykrycie czy jakis punkt nalezy do obb czy nie, dziala poprawnie i jest bardzo prosty w implementacji.

Tymczasem link do programu + zrodla: www.wachu.i365.pl/obb_test.rar

Plany na przyszlosc sa nastepujace, tzn. mozliwe drogi rozwoju:

• trzeba znalesc 3 metryke laczaca te 2 w ktorej bedzie mozna testowac kolizje obb
• mozna sprobowac rozwiazac uklad rownan: poszukac punktow dla ktorych odleglosc od jednej i drugiej kulki sa odpowiednio r1 i r2
  

Czesc, dzisiaj bedzie kolejna czesc zastosowania przestrzeni metrycznych. Wczoraj przeprowadzilem krotka dyskusje na ten temat z moim kolega aod'em i doszlismy do wniosku ze warto rozwinac ten temat. To co tutaj dzisiaj przedstawie nie zostalo przezemnie udowodnione i raczej nalezy to traktowac jako ciekawostke.

Jak mowilem ostatnio przy odpowiednim zdefiniowaniu metryki moze ona sie przydac do wielu roznych rzeczy. Zacznijmy od wprowadzenia definicji kuli:

• K(p, r) = { x: d(p, x) < r }
  

Jak widac jest to zbior punktow oddalonych od punktu p o promien r w metryce d. Wiemy rowniez ze jesli zmienimy metryke kula wcale nie musi byc okragla a na przyklad moze byc kwadratem.

Skoro tak to wpadlem na pomysl na nowe podejscie do rozwiazanie problemu kolizji dwoch obb (oriented bounding box) .

Kazdy OBB mozna przedstawic za pomoca kata obrotu, pozycji i promienia (dzisial bede mowil tylko o kwadratach). Teraz pojawia sie problem jak wygladalaby metryka w ktorej kula moglaby wygladac jak dowolny obb. Zmodyfikujmy troche metryke maksimum (zalozmy srodek w punkcie a i kat obrotu φ):

• d(a, b) = max{ |(a.x - b.x) cos(-φ) - (a.x - b.x) sin(-φ)| ,
  |(a.y - b.y) sin(-φ) + (a.y - b.y)cos(-φ)| }

Kolejny problem jaki sie pojawia to taki ze skoro mamy jedna metryke to narazie mozemy testowac kolizje tylko z obiektami ktore maja ta sama metryke.

I ten punkt musi byc jeszcze dopracowany, bo nie znam odpowiedzi na pytanie jak sprawdzac przeciecia kul w roznych metrykach.

To o czym tutaj powiedzialem to tylko moje domysly i pewne wyczucie.

Witam ponownie, tak jak powiedzialem ostatnio dzisiaj bedzie o liczabach zespolonych. Pomysl na napisanie kilku slow na ten temat podsnal mi moj kolega. Do rzeczy...

Za pomoca liczb zespolonych mozna w bardzo latwy sposob przedstawic obrot punktu wokol osi o podany kat. Wikipedia mowi nawet ze liczby zespolone mozna traktowac jak szczegolny przypadek kwaternionow. Zbadalem troche jak takie obroty mialyby wygladac i oto rezultaty.

Kazda liczbe zespolona najczesciej przedstawia sie w postaci: z = a + ib. Gdzie ReZ = a, ImZ = b (czesc rzeczywista i czesc urojona). Liczby rzeczywiste zawieraja sie w zbiorze liczb zespolonych i wystepuja w takiej postaci: a + i0.



Wprowadzmy teraz kilka oznaczen i definicji.

• sprzezenie liczby z = a - ib
• ArgZ mozemy interpretowac jako kat pomiedzy wektorem (a, b) i prosta OX
• modul liczby z oznaczamy przez |z| = sqrt( a² + b² )

Liczbe zespolona mozna przedstawic w postaci trygonometrycznej:

• z = | z | ( cos φ + isin φ )

Mnozenie liczb zespolonych wyraza sie wzorem (postac trygonometryczna):

• z1 * z2 = | z1 || z2 | ( cos (φ1 + φ2) + isin (φ1 + φ2) )

φ1, φ2 - sa to kolejno Arg z1 i Arg z2.

Teraz mozemy przejsc do liczenia obrotow. Jak widac ze wzoru na mnozenie liczb zespolonych w postaci trygonometrycznej jesli modul jednej z liczb jest rowny 1 to wynikiem bedzie "obrot punktu" o kat φ (bez zmieniania "odleglosci tego punktu od osi obrotu").

Teraz pojawia sie problem jak obrocic jakis punkt znajac tylko kat o jaki chcemy go obrocic i jego pozycje? Wystarczy odpowiednio przeksztalcic ponizsze wzory:

cosφ = a / |z|
sinφ = b / |z|

Mamy wiec wszystkie dane do wzoru na mnozenie liczb zespolonych w postaci trygonometrycznej. Jest jednak jeszcze jeden sposob na pomnozenie dwoch liczb zespolonych, bardziej tradycyjny:

(a, b) * (c, d) = (ac - bd, ad + bc)

przeksztalcamy wzory:

a = |z|cosφ
b = |z|sinφ

i podstawiamy spowrotem do wzoru na mnozenie:

(a, b) * (|z|cosφ, |z|sinφ) = (a|z|cosφ - b|z|sinφ, a|z|sinφ + b|z|cosφ)

W ten sposob mamy gotowy wzor na obrot punktu wokol punktu (0, 0). Obrot wokol dowolnego punktu mozna zrobic przez przesuciecie punktu do (0, 0), obrot i ponowne przesuniecie.

Wada przedstawiania obrotow na liczbach zespolonych jest to ze kat o jaki mozna obrocic punkt musi byc z przedzialu [0, 360). Oczywiscie przy odrobinie kreatywnosci mozna i ten problem przeskoczyc.

Najwieksza zaleta? Pozbycie sie macierzy z przestrzeni dwu wymiarowej, gdzie stosunek ich rozmiaru do zastosowania przechyla sie za bardzo na ich nie korzysc (wystarczy popatrzec na powyzsze wzory i pomyslec jak bardzo mozna je zoptymalizowac).

Witam, dzisiaj nie będzie tak jak zapowiadałem o texturowaniu terenu, a o matematyce :) Przez ostatni rok studiowałem ten przedmiot na Politechnice Warszawskiej i mimo tego, żę 99% rzeczy mi sie nie przyda w programowaniu o tyle chce dzisiaj powiedziec o czyms co niektórym sie moze przydac. Dzisiaj bedzie o: przestrzeniach metrycznych.

Kazdy mial kontakt z przestrzeniami metrycznymi chociaz pewnie nawet sobie z tego nie zdawal sprawy. Najczesciej spotykana metryka jest metryka euklidesowa czyli wszystkim znany wzor na odlegosc dwuch punktow od siebie: d(x, y) = sqrt( (a.x - b.x)² + (a.y - b.y)² ).

Jak widac odleglosc jest zdefiniowana jako funkcja. Skoro mozna ja zdefiniowac tak to mozna tez inaczej, jednak nowa funkcja musi spelniac nastepujace warunki:

1. d(x,y)=0 wtedy i tylko wtedy, gdy x=y
2. d(x,y)=d(y,x)
3. d(x,z) ≤ d(x,y)+d(y,z) (tzw. nierówność trójkąta).

Postaram sie teraz przedstawic kilka najpopularniejszych metryk:

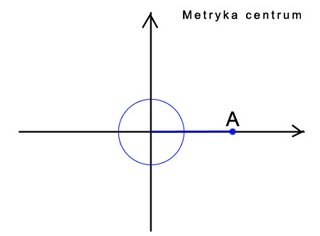
• metryka centrum (oznaczmy przez dE metryke euklidesowa): d(a, b) = dE(0, a) + dE(0, b)
• metryka dyskretna: d(a, b) = { 1 - jesli a != b; 0 - jesli a = b}
• metryka Manhattan: d(a, b) = |a.x - b.x| + |a.y - b.y|
• metryka maksimum: d(a, b) = max{ |a.x - b.x|, |a.y - b.y| }

Zastosowanie metryk:

• czesto na forach jest zadawane pytanie, jak w grach o widoku izometrycznym sprawdzic w ktore pole kliknieto. Jesli troche zmodyfikujemy metryke Manhattan bedziemy mieli latwa odpowiedz na to pytanie
• metryka maksimum tez jest bardzo ciekawa, bo mozna latwo sprawdzic czy cos lezy wewnatrz jakiegos kwadratu(po drobnych zmianach rowniez prostokat)
• najtrudniej znalezc zastosowanie dla metryki centrum, postac jaka zaprezentowalem powyzej jest malo przydatna (szczegolnie z mierzeniem odleglosci od punktu (0, 0)), jednak mozna ja bardziej uogolnic. Teraz nie znajduje dla niej zastosowania ale jakies jest napewno :)

Na jutro moze napisze cos o liczbach zespolonych i ich wykorzystaniu w reprezenatacji obrotow.