Wachu - DevLog

Witam, dzisiaj nie będzie tak jak zapowiadałem o texturowaniu terenu, a o matematyce :) Przez ostatni rok studiowałem ten przedmiot na Politechnice Warszawskiej i mimo tego, żę 99% rzeczy mi sie nie przyda w programowaniu o tyle chce dzisiaj powiedziec o czyms co niektórym sie moze przydac. Dzisiaj bedzie o: przestrzeniach metrycznych.

Kazdy mial kontakt z przestrzeniami metrycznymi chociaz pewnie nawet sobie z tego nie zdawal sprawy. Najczesciej spotykana metryka jest metryka euklidesowa czyli wszystkim znany wzor na odlegosc dwuch punktow od siebie: d(x, y) = sqrt( (a.x - b.x)² + (a.y - b.y)² ).

Jak widac odleglosc jest zdefiniowana jako funkcja. Skoro mozna ja zdefiniowac tak to mozna tez inaczej, jednak nowa funkcja musi spelniac nastepujace warunki:

1. d(x,y)=0 wtedy i tylko wtedy, gdy x=y
2. d(x,y)=d(y,x)
3. d(x,z) ≤ d(x,y)+d(y,z) (tzw. nierówność trójkąta).

Postaram sie teraz przedstawic kilka najpopularniejszych metryk:

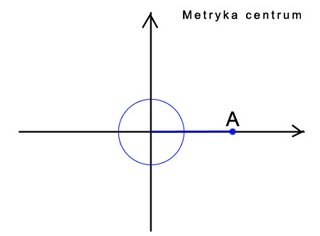
• metryka centrum (oznaczmy przez dE metryke euklidesowa): d(a, b) = dE(0, a) + dE(0, b)
• metryka dyskretna: d(a, b) = { 1 - jesli a != b; 0 - jesli a = b}
• metryka Manhattan: d(a, b) = |a.x - b.x| + |a.y - b.y|
• metryka maksimum: d(a, b) = max{ |a.x - b.x|, |a.y - b.y| }

Zastosowanie metryk:

• czesto na forach jest zadawane pytanie, jak w grach o widoku izometrycznym sprawdzic w ktore pole kliknieto. Jesli troche zmodyfikujemy metryke Manhattan bedziemy mieli latwa odpowiedz na to pytanie
• metryka maksimum tez jest bardzo ciekawa, bo mozna latwo sprawdzic czy cos lezy wewnatrz jakiegos kwadratu(po drobnych zmianach rowniez prostokat)
• najtrudniej znalezc zastosowanie dla metryki centrum, postac jaka zaprezentowalem powyzej jest malo przydatna (szczegolnie z mierzeniem odleglosci od punktu (0, 0)), jednak mozna ja bardziej uogolnic. Teraz nie znajduje dla niej zastosowania ale jakies jest napewno :)

Na jutro moze napisze cos o liczbach zespolonych i ich wykorzystaniu w reprezenatacji obrotow.