Wachu - DevLog

Czesc, dzisiaj bedzie kolejna czesc zastosowania przestrzeni metrycznych. Wczoraj przeprowadzilem krotka dyskusje na ten temat z moim kolega aod'em i doszlismy do wniosku ze warto rozwinac ten temat. To co tutaj dzisiaj przedstawie nie zostalo przezemnie udowodnione i raczej nalezy to traktowac jako ciekawostke.

Jak mowilem ostatnio przy odpowiednim zdefiniowaniu metryki moze ona sie przydac do wielu roznych rzeczy. Zacznijmy od wprowadzenia definicji kuli:

• K(p, r) = { x: d(p, x) < r }
  

Jak widac jest to zbior punktow oddalonych od punktu p o promien r w metryce d. Wiemy rowniez ze jesli zmienimy metryke kula wcale nie musi byc okragla a na przyklad moze byc kwadratem.

Skoro tak to wpadlem na pomysl na nowe podejscie do rozwiazanie problemu kolizji dwoch obb (oriented bounding box) .

Kazdy OBB mozna przedstawic za pomoca kata obrotu, pozycji i promienia (dzisial bede mowil tylko o kwadratach). Teraz pojawia sie problem jak wygladalaby metryka w ktorej kula moglaby wygladac jak dowolny obb. Zmodyfikujmy troche metryke maksimum (zalozmy srodek w punkcie a i kat obrotu φ):

• d(a, b) = max{ |(a.x - b.x) cos(-φ) - (a.x - b.x) sin(-φ)| ,
  |(a.y - b.y) sin(-φ) + (a.y - b.y)cos(-φ)| }

Kolejny problem jaki sie pojawia to taki ze skoro mamy jedna metryke to narazie mozemy testowac kolizje tylko z obiektami ktore maja ta sama metryke.

I ten punkt musi byc jeszcze dopracowany, bo nie znam odpowiedzi na pytanie jak sprawdzac przeciecia kul w roznych metrykach.

To o czym tutaj powiedzialem to tylko moje domysly i pewne wyczucie.

Witam ponownie, tak jak powiedzialem ostatnio dzisiaj bedzie o liczabach zespolonych. Pomysl na napisanie kilku slow na ten temat podsnal mi moj kolega. Do rzeczy...

Za pomoca liczb zespolonych mozna w bardzo latwy sposob przedstawic obrot punktu wokol osi o podany kat. Wikipedia mowi nawet ze liczby zespolone mozna traktowac jak szczegolny przypadek kwaternionow. Zbadalem troche jak takie obroty mialyby wygladac i oto rezultaty.

Kazda liczbe zespolona najczesciej przedstawia sie w postaci: z = a + ib. Gdzie ReZ = a, ImZ = b (czesc rzeczywista i czesc urojona). Liczby rzeczywiste zawieraja sie w zbiorze liczb zespolonych i wystepuja w takiej postaci: a + i0.



Wprowadzmy teraz kilka oznaczen i definicji.

• sprzezenie liczby z = a - ib
• ArgZ mozemy interpretowac jako kat pomiedzy wektorem (a, b) i prosta OX
• modul liczby z oznaczamy przez |z| = sqrt( a² + b² )

Liczbe zespolona mozna przedstawic w postaci trygonometrycznej:

• z = | z | ( cos φ + isin φ )

Mnozenie liczb zespolonych wyraza sie wzorem (postac trygonometryczna):

• z1 * z2 = | z1 || z2 | ( cos (φ1 + φ2) + isin (φ1 + φ2) )

φ1, φ2 - sa to kolejno Arg z1 i Arg z2.

Teraz mozemy przejsc do liczenia obrotow. Jak widac ze wzoru na mnozenie liczb zespolonych w postaci trygonometrycznej jesli modul jednej z liczb jest rowny 1 to wynikiem bedzie "obrot punktu" o kat φ (bez zmieniania "odleglosci tego punktu od osi obrotu").

Teraz pojawia sie problem jak obrocic jakis punkt znajac tylko kat o jaki chcemy go obrocic i jego pozycje? Wystarczy odpowiednio przeksztalcic ponizsze wzory:

cosφ = a / |z|
sinφ = b / |z|

Mamy wiec wszystkie dane do wzoru na mnozenie liczb zespolonych w postaci trygonometrycznej. Jest jednak jeszcze jeden sposob na pomnozenie dwoch liczb zespolonych, bardziej tradycyjny:

(a, b) * (c, d) = (ac - bd, ad + bc)

przeksztalcamy wzory:

a = |z|cosφ
b = |z|sinφ

i podstawiamy spowrotem do wzoru na mnozenie:

(a, b) * (|z|cosφ, |z|sinφ) = (a|z|cosφ - b|z|sinφ, a|z|sinφ + b|z|cosφ)

W ten sposob mamy gotowy wzor na obrot punktu wokol punktu (0, 0). Obrot wokol dowolnego punktu mozna zrobic przez przesuciecie punktu do (0, 0), obrot i ponowne przesuniecie.

Wada przedstawiania obrotow na liczbach zespolonych jest to ze kat o jaki mozna obrocic punkt musi byc z przedzialu [0, 360). Oczywiscie przy odrobinie kreatywnosci mozna i ten problem przeskoczyc.

Najwieksza zaleta? Pozbycie sie macierzy z przestrzeni dwu wymiarowej, gdzie stosunek ich rozmiaru do zastosowania przechyla sie za bardzo na ich nie korzysc (wystarczy popatrzec na powyzsze wzory i pomyslec jak bardzo mozna je zoptymalizowac).

Witam, dzisiaj nie będzie tak jak zapowiadałem o texturowaniu terenu, a o matematyce :) Przez ostatni rok studiowałem ten przedmiot na Politechnice Warszawskiej i mimo tego, żę 99% rzeczy mi sie nie przyda w programowaniu o tyle chce dzisiaj powiedziec o czyms co niektórym sie moze przydac. Dzisiaj bedzie o: przestrzeniach metrycznych.

Kazdy mial kontakt z przestrzeniami metrycznymi chociaz pewnie nawet sobie z tego nie zdawal sprawy. Najczesciej spotykana metryka jest metryka euklidesowa czyli wszystkim znany wzor na odlegosc dwuch punktow od siebie: d(x, y) = sqrt( (a.x - b.x)² + (a.y - b.y)² ).

Jak widac odleglosc jest zdefiniowana jako funkcja. Skoro mozna ja zdefiniowac tak to mozna tez inaczej, jednak nowa funkcja musi spelniac nastepujace warunki:

1. d(x,y)=0 wtedy i tylko wtedy, gdy x=y
2. d(x,y)=d(y,x)
3. d(x,z) ≤ d(x,y)+d(y,z) (tzw. nierówność trójkąta).

Postaram sie teraz przedstawic kilka najpopularniejszych metryk:

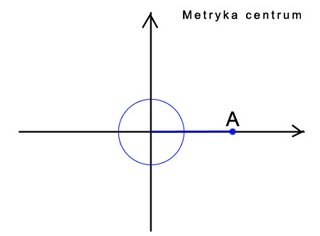
• metryka centrum (oznaczmy przez dE metryke euklidesowa): d(a, b) = dE(0, a) + dE(0, b)
• metryka dyskretna: d(a, b) = { 1 - jesli a != b; 0 - jesli a = b}
• metryka Manhattan: d(a, b) = |a.x - b.x| + |a.y - b.y|
• metryka maksimum: d(a, b) = max{ |a.x - b.x|, |a.y - b.y| }

Zastosowanie metryk:

• czesto na forach jest zadawane pytanie, jak w grach o widoku izometrycznym sprawdzic w ktore pole kliknieto. Jesli troche zmodyfikujemy metryke Manhattan bedziemy mieli latwa odpowiedz na to pytanie
• metryka maksimum tez jest bardzo ciekawa, bo mozna latwo sprawdzic czy cos lezy wewnatrz jakiegos kwadratu(po drobnych zmianach rowniez prostokat)
• najtrudniej znalezc zastosowanie dla metryki centrum, postac jaka zaprezentowalem powyzej jest malo przydatna (szczegolnie z mierzeniem odleglosci od punktu (0, 0)), jednak mozna ja bardziej uogolnic. Teraz nie znajduje dla niej zastosowania ale jakies jest napewno :)

Na jutro moze napisze cos o liczbach zespolonych i ich wykorzystaniu w reprezenatacji obrotow.

Ostatnio troche czasu spedzilem nad tworzeniem oswietlenia do mojego silnika i chcialbym dzisiaj zaprezentowac moje przemyslenia na ten temat.

Zalozenia jakie sobie postawilem byly dosc proste: swiatla punktowe w dowolnym kolorze, oswietlajace tylko te obiekty ktore sa pod nimi i pozostawiajace nie oswietlone te obiekty ktore sa "wyzsze od swiatla", do tego wszystkiego chcialem zrobic cienie. "Wyzsze od swiatel" jest umowne bo moj silnik jest przeznaczony dla gier 2d z widokiem z gory, wiec tak naprawde nie ma sposobu na okreslenie wysokosci obiektow.

Pierwszym problem jaki napotkalem bylo jak zrobic zeby obszar gdzie nie ma swiatla byl zaciemniony? Zrobilem to tak ze najpierw renderuje wszystkie obiekty normalnie, pozniej renderuje swiatla do textury. Robie to w ten sposob ze podmieniam tylko backbuffer natomiast zbuffer pozostawiam bez zmian. Przed renderowaniem swiatel czyszcze caly ekran na jakis okreslony kolor ktory przyjmuje za brak oswietlenia.
Pozostawiajac Z buffor wypelniony wartosciami Z obiektow mam pewnosci ze beda oswietlone tylko te obiekty ktore sa pod swiatlem, a obiekty nad swiatlem pozostana nie oswietlone.
Oto stany mieszania jakich uzywam (DirectX 9):

engine->setRenderState(D3DRS_SRCBLEND, D3DBLEND_ONE);
engine->setRenderState(D3DRS_DESTBLEND, D3DBLEND_ONE);

Uzylem, D3DBLEND_ONE poniewaz w rzeczywistosci miejsca oswietlane przez dwa swiatla sa bardziej oswietlone niz te oswietlone tylko jednym swiatlem.

Po wyrenderowaniu wszystkich swiatel, wyswietlam texture do ktorej renderowalem na calym ekranie. Z takim mieszaniem kolorow:

engine->setRenderState(D3DRS_SRCBLEND, D3DBLEND_ZERO); engine->setRenderState(D3DRS_DESTBLEND, D3DBLEND_SRCCOLOR);

Dzieki temu powstaje odpowiedni efekt oswietlenia.

Kolejnym punktem jaki chcialem zrealizowac to rzucanie cieni. W obecnej wersji cienie nie sa rzucane przez mesh, a przez obiekt Collidera (z tego wzgledu ze jako jedyny ma wyroznione krawedzie).

Na tym screenie widac poprawnie wyswietlony cien:














Obiekt z duza czerwona kropka jest wyzszy od pozostalych i jak widac poprawnie rzuca na nie cien. Pozostale obiekty sa na tej samej wysokosci i nie rzucaja na siebie cieni.

Rzucanie cieni odbywa sie w ten sposob, ze bierzemy obiekt i swiatlo. Znajdujemy wszystkie krawedzie dla ktorych iloczyn skalarny wektora z pozycji swiatla do srodka krawedzi i normalnej dla tej krawedzi jest > 0. Na podstawie tych krawedzi dodajemy dodatkowe trojkaty przedstawiajace rzucany cien. Dlugosc cienia jest wprost proporcjonalna do odleglosci od zrodla swiatla. W kilku artykulach na sieci widzialem, ze wystepuje problem gdy zrodlo swiatla zawiera sie w obiekcie. U mnie jest to tak rozwiazane wlasnie przez okreslanie dlugosci cienia oraz zalozenia ze swiatlo jest zawsze nad obiektem (nawet jesli teoretycznie leza na tej samej plaszczyznie).

Kolejnym problemem jaki trzeba rozwiazac przy rzucaniu cieni jest obszar pozbawiony swiatla bardzo rzadko jest w stu procentach czarny (moze byc np. poranek lub wieczor) wiec jesli obiekt bedzie na granicy zasiegu swiatla bedzie rzucal cien ale sam cien bedzie juz poza zasiegiem i bedzie tworzyl dziwny efekt przyciemniania obszaru gdzie nie ma swiatla. Moim rozwiazaniem jest wprowadzenie przezroczystosci cienia w zaleznosci od odleglosci od zrodla swiatla. Jesli cien jest na granicy dzialania swiatla to jest calkowicie przezroczysty. Oprocz tego wprowadzilem brak przezroczystosci cienia najblizej obiektu i prawie calkowita przezroczystosc w obszarze najbardziej oddalonym od obiektu.

Ostatecznie otrzymalem taki dosc ladny jak mi sie wydaje efekt:

Witam, dzisiaj chciałbym napisać o fizyce 2d bryły sztywnej którą ostatnio implementowałem.

Pierwszym problemem jaki trzeba bylo rozwiacac to sprawdzanie kolizji OBB ( oriented bounding box ). W sieci znalazlem bardzo dobry artykuł na ten temat, a konkretniej wykrywanie kolizji za pomoca SAT (separate axis teorem). Algorytm ten gwarantuje nie tylko wykrycie kolizji ale rowniez sposob reakcji (minimalny wektor o jaki trzeba odsunac dwa obiekty zeby ze soboa nie kolidowaly).

Zastosowanie tego algorytmu w moim silniku przedstawia sie mniej wiecej tak: kazdy obiekt jest dziedziczony po klasie iActor ktora implementuje podstawowe wlasciwoscie fizyczne takie jak masa, bezwladnosc, predkosc katowa, predkosc liniowa itp. oraz udostepnia interfejs do aplikowania nowych sil dzialajacych na ten obiekt. Kazdy obiekt ktory jest poddawany sprawdzaniu kolizji zawiera obiekt klasy Collider, ktora opisuje ksztalt naszego obiektu (lista krawedzi). Kolizje sa sprawdzane przez podanie pary obiektow do klasy CollisionCheck. W rezultacie dostajemy informacje czy kolizja zachodzi jesli tak to mamy rowniez takie dane: normalna punktu kolizji, punkt kolizji, minimalne przesuniecie o jakie trzeba dwa obiekty od siebie odsunac.

Fizyczna reakcja na kolizje zajmuje sie klasa Physics ktora co staly okres czasu aktualizuje symulacje fizyczna. Materialy ktore mi poslozyly do opisanie relistycznego zachowania sie obiektów znalazlen na tej stronie. Autor jednak nie przewidzial sily tarcia ktora dziala podczas zderzenia i ten element wzoru wyprowadzilem sam. Konkretniej, rzutowalem wektor predkosci po kolizji na prosta prostopadla do normalnej kolizji i przemnozylem przez wspolczynnik tarcia, odejmujac otrzymany wektor od wektora predkosci po kolizji.

Prezentacje jak ta fizyka sie sprawuje w dzialaniu mozna zobaczyc na tym krotkim filmiku (na ktorym jednak nie ma jeszcze zaimplementowanego tarcia).

Witam w moim devlogu! Będę tutaj prezentował postepy w mojej pracy programistycznej. Zachęcam do czytania!

Witam w moim devlogu! Będę tutaj prezentował postepy w mojej pracy programistycznej. Zachęcam do czytania!